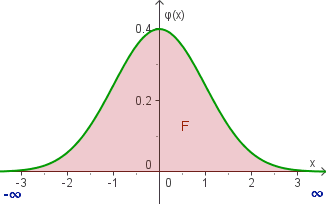
F = Φ(∞) = 1
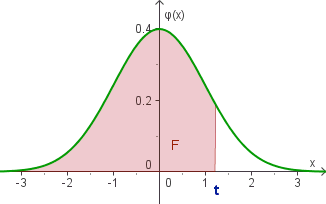
F = Φ(t)

F = 1 − Φ(t)
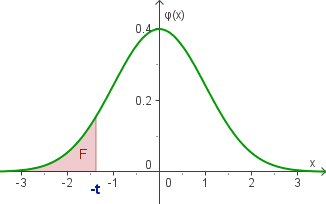
F = Φ(−t) = 1 − Φ(t)
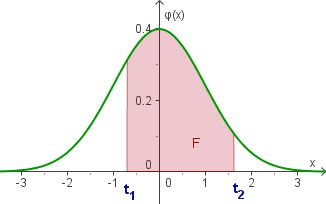
F = Φ(t2) − Φ(t1)
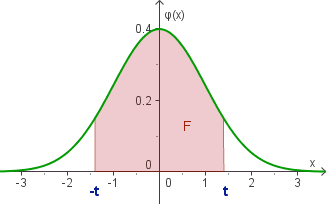
F = Φ(t) − Φ(−t) = 2 · Φ(t) − 1
Die Gaußsche Integralfunktion Φ misst die linke Randfläche unter der Glockenkurve der Dichtefunktion φ. Φ ist also die zu φ gehörende Verteilungsfunktion und Integralfunktion von φ.
Φ lässt sich nicht durch elementare Funktionen ausdrücken. Man kann sie jedoch mit Hilfe numerischer Methoden beliebig genau berechnen und tabellieren. Die Bestimmung von Wahrscheinlichkeiten mit Hilfe der Integralfunktion Φ reduziert sich auf die Berechnung verschiedener Flächentypen:

F = Φ(∞) = 1 |

F = Φ(t) |

F = 1 − Φ(t) |

F = Φ(−t) = 1 − Φ(t) |

F = Φ(t2) − Φ(t1) |

F = Φ(t) − Φ(−t) = 2 · Φ(t) − 1 |
P(k1 ≤ X ≤ k2) ≈ Φ[(k2 + 0,5 − μ) / σ] − Φ[(k1 − 0,5 − μ) / σ].
Integrale Näherungsformel von de Moivre-Laplace